变分推断

2025-03-07

/

https://www.zhihu.com/question/41765860

我们常用的贝叶斯公式求后验分布 $P(Z|X)$ 的时候常用

P(Z|X)=\frac{p(X,Z)}{\int_zp(X,Z=z)dz}

但是这里使用贝叶斯求解是很困难的，因为我们的积分 z 通常是一个高维随机变量。在贝叶斯统计中，所有对于未知量推断的问题可以看作是对后验概率的计算，因此提出了变分推断来计算后验概率。

他的思想主要包括：

假设一个分布 $q(z;\lambda)$
通过改变分布的参数 $\lambda$ 来使得我们假设的分布尽可能靠近 $p(z|x)$ 一言以蔽之，就是为真实的后验分布引入了一个参数化的模型，也就是用简单的分布来拟合复杂的分布，这种计算测率将计算 $p(x|z)$ 转化为了优化问题：

\lambda^*=\arg\min_\lambda\operatorname{divergence}(p(z|x),q(z;\lambda))

这里就是求 kl 散度最小

求解#

首先是一个公式的等价转换

\begin{aligned} \log P(x) & =\log P(x,z)-\log P(z|x) \\ & =\log\frac{P(x,z)}{Q(z;\lambda)}-\log\frac{P(z|x)}{Q(z;\lambda)} \end{aligned}

两边同时对 $Q(z)$ 求期望得到

\begin{aligned} \mathbb{E}_{q(z;\lambda)}\log P(x) & =\mathbb{E}_{q(z;\lambda)}\left.\log P(x,z)-\mathbb{E}_{q(z;\lambda)}\right.\log P(z|x) \\ \log P(x) & =\mathbb{E}_{q(z;\lambda)}\log\frac{p(x,z)}{q(z;\lambda)}-\mathbb{E}_{q(z;\lambda)}\log\frac{p(z|x)}{q(z;\lambda)} \\ & =KL(q(z;\lambda)\|p(z|x))+\mathbb{E}_{q(z;\lambda)}\log\frac{p(x,z)}{q(z;\lambda)} \\ \log P(x) & =KL(q(z;\lambda)\|p(z|x))+\mathbb{E}_{q(z;\lambda)}\log\frac{p(x,z)}{q(z;\lambda)} \end{aligned}

TIP
https://blog.csdn.net/mch2869253130/article/details/108998463
kl 散度的公式为: $D_{KL}(p\|q)=\sum_{i=1}^Np\left(x_i\right)\log\left(\frac{p\left(x_i\right)}{q\left(x_i\right)}\right)$ ,是使用后面的分布近似前面的，而反向 kl 散度是用前面的近似后面的. 两者的区别在于：对于正向 kl 散度，想要最小化 kl 散度，在 $px$ 大的地方需要 $qx$ 也大而在 $px$ 小的地方 $qx$ 没有太多影响，所以得到的是一个较宽的分布。而对于反向 kl 散度，在 $px$ 大的地方可以忽略，而在 $px$ =0 的地方 $qx$ 也要趋向于 0，也就是得到一个较窄的分布。
例子：假设现在有一个两个高斯分布混合的 px,qx 是单个高斯，用 qx 来近似 px，下面两种 kl 散度如何选择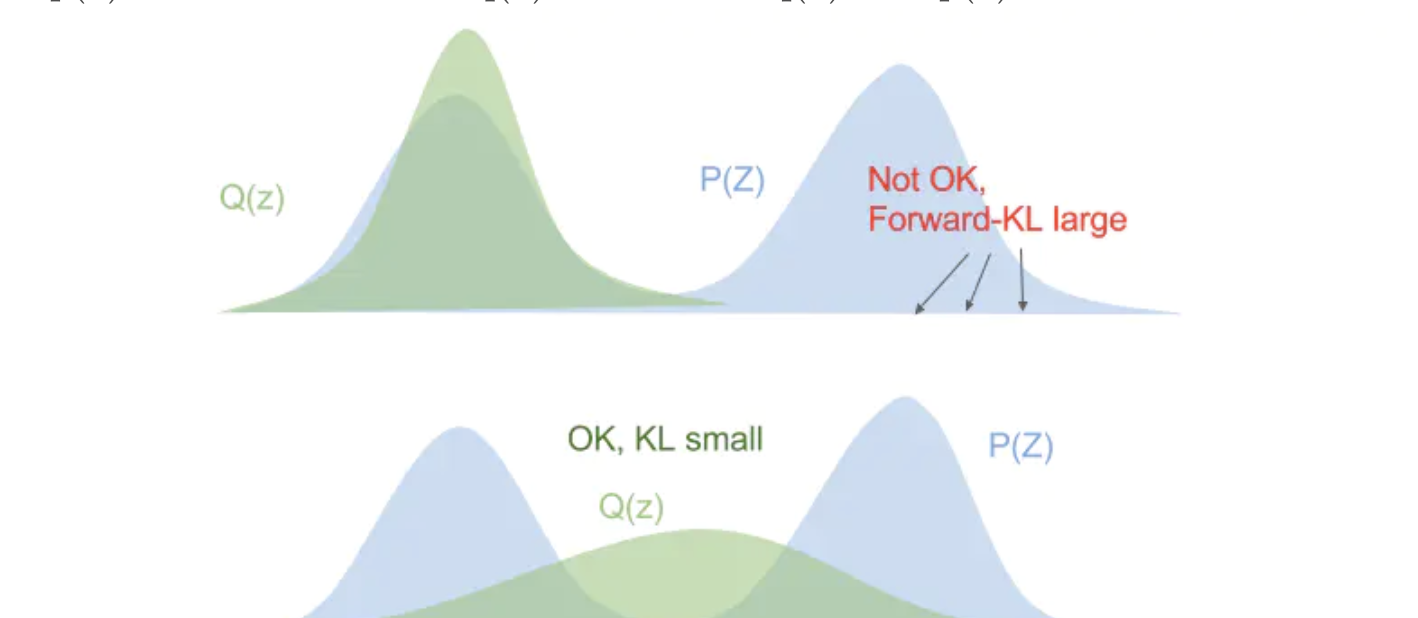？对于正向来说，他选择第二个，它更在意常见事件，当 p 有多个峰的时候，q 选择把这些峰模糊在一起。而对于反向 kl 散度来说，qx 的分布更符合第二行，反向 kl 散度更在意 px 中的罕见事件，保证符合低谷的事件。

回到我们前面的问题，我们的目标就是最小化 q 对 p 的 kl 散度,为了最小化 kl 散度，也就是求解 (这里使用了反向 kl 散度)

\max_{\lambda}\mathbb{E}_{q(z;\lambda)}\mathrm{log}\frac{p(x,z)}{q(z;\lambda)}=ELBO

这里的 $p(x)$ 一般被称为 evidence，又因为 kl 散度大于 0，所以 $logp(x)\geq E_{q(z;\lambda)}\left[ \log \frac{p(x,z)}{\log q(z;\lambda)} \right]$

所以最后的公式为：

\log(P(x))=KL(q(z;\lambda)||p(z|x)+ELBO

EM 算法就是利用了这一特征，但是 EM 算法假设了 p(z|x) 是易于计算的形式，变分则无这一限制。

黑盒变分推断（BBVI）#

对于 ELBO 公式，使用参数 $\theta$ 代替 $\lambda$ ,并对其求导

\nabla_\theta\operatorname{ELBO}(\theta)=\nabla_\theta\mathbb{E}_q\left(\log p(x,z)-\log q_\theta(z)\right)

展开计算的到

\begin{aligned} & \frac{\partial}{\partial\theta}\int q_\theta(z)\left(\log p(x,z)-\log q_\theta(z)\right)dz \\ & =\int\frac{\partial}{\partial\theta}[q_\theta(z)\left(\log p(x,z)-\log q_\theta(z)\right)]dz \\ & =\int\frac{\partial}{\partial\theta}(q_\theta(z)\log p(x,z))-\frac{\partial}{\partial\theta}(q_\theta(z)\log q_\theta(z))dz \\ & =\int\frac{\partial q_{\theta}(z)}{\partial\theta}{\log p(x,z)}-\frac{\partial q_{\theta}(z)}{\partial\theta}{\log q_{\theta}(z)}-\frac{\partial q_{\theta}(z)}{\partial\theta}dz \end{aligned}

因为

\int\frac{\partial q_\theta(z)}{\partial\theta}dz=\frac{\partial}{\partial\theta}\int q_\theta(z)dz=\frac{\partial}{\partial\theta}1=0

所以

\begin{aligned} \nabla_\theta\operatorname{ELBO}(\theta) & =\int\frac{\partial q_\theta(z)}{\partial\theta}(\log p(x,z)-\log q_\theta(z))dz \\ & =\int q_\theta(z)\frac{\partial\log q_\theta(z)}{\partial\theta}(\log p(x,z)-\log q_\theta(z))dz \\ & =\int q_\theta(z)\nabla_\theta\log q_\theta(z)\left(\log p(x,z)-\log q_\theta(z)\right)dz \\ & =\mathbb{E}_q\left[\nabla_\theta\log q_\theta(z)\left(\log p(x,z)-\log q_\theta(z)\right)\right] \end{aligned}