Abstract
多模态学习通常依赖于假设:训练和推理阶段所有的模态都是可用的.但在真实生活中完全获得全部的多模态数据非常困难,这通常会导致确实模态的问题这不仅对多模态预训练模型的可用性构成了巨大的障碍,还对其微调和下游任务的鲁棒性保持提出了挑战。为了应对这个问题,我们提出了一种新颖的架构,把单模态预训练模型的参数高效微调方法和自监督联合嵌入方法结合,这个架构能让模型预测缺失模态在特征空间中的表示.
Introduction
缺失数据的情况非常常见,且单模态的数据获得比较方便
在本文中,我们定义多模态设置问题如下:
- 假设存在单模态的预训练模型
- 下游任务提供了不完全配对的数据
- 不配对的数据在推理的时候也提供了. 在这种情况下,我们提出了一种高效的框架来解决缺失模态问题通过使用预训练模型和预测缺失模态的表示.我们的贡献如下:
- 使用参数高效的微调(PEFT)来最小化单模态预训练模型的训练并且最大化为下游任务的知识展现
- 我们使用方差-不变性-协方差架构,来提升不同模态对于缺失模态问题的可预测性
- 我们采用了一种基于提示的方法来从其他的模态中高效的聚集任务相关的信息
- 我们的方法被证明是有效的
Preliminaries
问题定义
为了保持简单并且不失一般性,我们只考虑两个模态,叫 m1 和 m2,我们还假设这俩模态并不一直存在,缺失模态在整个训练周期中都存在,因此,给定一个多模态数据集,能够分为 3 个子数据集,分别是完全模态数据集 Dc,和两盒模态不完全子集 Da 和 Db
基于这个假设,我们还假设没有预先训练的多模态 encoder,此外,每个模态都有自己的预训练 encoder 在自己的单模态数据集上被训练.基于此,我们可以聚集在更为普遍的问题上.
如图 1(a)和(b)所示,对于每个模态,我们假设他们基于 Transformer 架构和足厚一层前是一个分类器.我们实现了一个晚融合策略,整合了每个模态的预测最大值.为了解决模态缺失带来的挑战,我们映入了一个特征预测器被用来预测缺失数据的特征.此外,为了加强预测能力,我们使用一组可训练的 prompt.
只读的 Prompts
为了增强预测其他模态的能力,更新 encoder 的参数或者训练新加入的参数是非常有必要的.但是,这样的更新可能会导致单模态 encoder 的高质量表示.prompt 微调是高效的策略,他向序列中输入可学习的 token 而不影响 encoder 的预训练权重,这种方法可以增加模型的适应能力同时保持原始的参数.然而,由于输入数据和提示词之间的注意力相互作用,传统的微调仍会影响原始的数据表示.为了解决这个问题,我们提出了只读的提示词策略,通过对自注意机制应用掩码策略,专门针对输入数据和提示令牌之间的交互,我们确保只有提示可以“读取”输入令牌特征。该方法保持了令牌特征不受提示影,使提示能够专注于提取在跨模态特征预测中所需的相关信息。因此,提示会专门用于该子任务,即特征预测。
Method
通过简单的后期融合策略进行多模态分类任务
尽管预训练的单模态 encoder 在不使用 fine-tune 的情况下仍然能够表现的很好,但是他们在特定的多模态任务中下游任务表现不是最优的.但是全参数微调也许提升了性能,但是消耗大量性能.因此我们使用 BitFit 作为 PEFT 方法,冻结模型的所有参数只更新偏置项.就这个设置,我们定义了多模态分类损失函数为多个模态上的标准交叉熵分类的损失之和
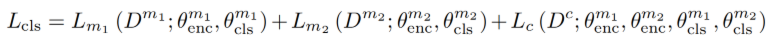
通过 prompt-Tuning 来进行缺失模态特征预测
我们引入了特征预测器使用可训练的参数来解决模态预测问题.我们使用只读的 prompt 来 concat 到单模态的输入数据中.具体来说,输入数据如下
其中 cls 和 embedding 都是不变的不论 prompt 怎么更改.基于这些输出,类别预测对于现有的模态 m 就可以预测出来了,并且还可以预测缺失模态 m’的特征.通过调整提示可以增强特征预测.
为了优化我们的特征预测,我们使用模态完全的数据集来模拟缺失.为了提高嵌入的可预测性,我们爱用VICReg的方法,基于此方法的损失函数用与预测嵌入表示.为了防止崩溃该损失函数由三部分组成.首先,方差项迫使批次中样本的嵌入向量彼此不同。它涉及一种铰链损失函数,维持嵌入在批次维度上的每个分量的标准差。其次,不变性项是主要目标,即计算原始特征和预测特征之间的均方欧几里得距离。最后,协方差项用于通过将嵌入协方差矩阵的非对角系数设为零来去相关化嵌入的不同维度。
其中s,v,c是invariance,方差,协方差
