Abstract# 通常的持续学习至今都使用了基于正则化的方法,这些方法都归结为依赖于模型权重的海森矩阵近似.但是这些方法在知识迁移和遗忘之间存在次优的均衡.另一类元持续学习方法要求先前的任务梯度和当前的任务梯度一致.在本文中,我们把元持续学习和正则化的方法连接起来,
Introduction# 持续学习在非平稳分布的数据集上进行训练,在 CL 中的 i.i.d 假设可能会导致在能行遗忘,引起先前的学习性能的下降
TIP i.i.d 是指一组随机变量中每个变量的概率分布都相同,且这些随机变量互相独立
今年来有许多的工作尝试解决灾难性遗忘,正则化方法是其中的一个重要分支,旨在保留和先前的任务相关的重要参数的权重以维持其性能.这些正则化方法的主要区别是他们对于近似海森矩阵的方法有所不同.尽管这些方法努力改进海森近似以保留先前任务的重要权重,但它们对先前任务估计的海森矩阵在后续训练中保持不变且无法更新。随着模型参数逐渐偏离最初计算海森矩阵的点,由于泰勒展开的截断误差增加,未改变的估计海森矩阵会逐渐失去准确性。
与在每个任务结束后显示的计算海森矩阵不同,元持续学习方法使用双层优化获得的超梯度隐式地利用二阶海森信息.超梯度的计算涉及从内存缓冲区中抽取的一批样本,该缓冲区存储了来自先前任务的样本,这使得 Meta-CL 能够利用来自先前任务的最新二阶信息。然而,值得注意的是,使用从内存缓冲区抽取的样本可能无法提供先前任务的完整表示,甚至可能缺乏某些任务的数据。这可能导致海森估计中存在错误信息。因此,隐式估计的海森矩阵可能存在相当大的变化,最终导致先前任务性能的下降。
基于正则化的持续学习的统一框架# 基于正则化的连续学习方法分析。连续学习考虑一个包含 N N N [ T 1 , T 2 , ⋯ , T N ] [T^1, T^2, \cdots, T^N] [ T 1 , T 2 , ⋯ , T N ] i i i N i N^i N i T i = ( X i , Y i ) = { ( x n i , y n i ) } n = 0 N i T^i = (\mathbf{X}^i, \mathbf{Y}^i) = \{(x_n^i, y_n^i)\}_{n=0}^{N^i} T i = ( X i , Y i ) = {( x n i , y n i ) } n = 0 N i T j T^j T j T [ 1 : j ] T^{[1:j]} T [ 1 : j ] j j j L i ( θ ) \mathcal{L}^i(\theta) L i ( θ ) θ \theta θ T i T^i T i θ \theta θ T [ 1 : j ] T^{[1:j]} T [ 1 : j ] 1 j ( ∑ i = 1 j L i ( θ ) ) \frac{1}{j}(\sum_{i=1}^{j} \mathcal{L}^i(\theta)) j 1 ( ∑ i = 1 j L i ( θ ))
然而,在基于正则化的连续学习(CL)中,我们无法访问先前学习任务 T [ 1 : j − 1 ] T^{[1:j-1]} T [ 1 : j − 1 ] θ \theta θ ∑ i = 1 j − 1 L i ( θ ) \sum_{i=1}^{j-1} \mathcal{L}^i(\theta) ∑ i = 1 j − 1 L i ( θ ) T j T^j T j j = 2 j=2 j = 2 T 2 T^2 T 2 1 2 ( L 1 prox + L 2 ) \frac{1}{2}(\mathcal{L}_1^{\text{prox}} + \mathcal{L}^2) 2 1 ( L 1 prox + L 2 ) L 1 prox ( θ ) \mathcal{L}_1^{\text{prox}}(\theta) L 1 prox ( θ ) θ ^ 1 \hat{\theta}^1 θ ^ 1 L 1 ( θ ) \mathcal{L}^1(\theta) L 1 ( θ )
L 1 prox = L 1 ( θ ^ 1 ) + ( θ − θ ^ 1 ) ⊤ ∇ L 1 ( θ ^ 1 ) + 1 2 ( θ − θ ^ 1 ) ⊤ ∇ 2 L 1 ( θ ^ 1 ) ( θ − θ ^ 1 ) \mathcal{L}_1^{\text{prox}} = \mathcal{L}^1(\hat{\theta}^1) + (\theta - \hat{\theta}^1)^\top \nabla \mathcal{L}^1(\hat{\theta}^1) + \frac{1}{2}(\theta - \hat{\theta}^1)^\top \nabla^2 \mathcal{L}^1(\hat{\theta}^1)(\theta - \hat{\theta}^1) L 1 prox = L 1 ( θ ^ 1 ) + ( θ − θ ^ 1 ) ⊤ ∇ L 1 ( θ ^ 1 ) + 2 1 ( θ − θ ^ 1 ) ⊤ ∇ 2 L 1 ( θ ^ 1 ) ( θ − θ ^ 1 ) 其中,θ ^ 1 \hat{\theta}^1 θ ^ 1 T 1 T^1 T 1 j > 2 j > 2 j > 2 ( j − 1 ) (j-1) ( j − 1 )
L j − 1 prox ( θ ) = ∑ i = 1 j − 1 L i ( θ ^ i ) ⏟ ( a ) + ( θ − θ ^ i ) ⊤ ∇ θ L i ( θ ^ i ) ⏟ ( b ) + 1 2 ( θ − θ ^ i ) ⊤ H i ( θ − θ ^ i ) ⏟ ( c ) (1) \mathcal{L}_{j-1}^{\text{prox}}(\theta) = \sum_{i=1}^{j-1} \underbrace{\mathcal{L}^i(\hat{\theta}^i)}_{(a)} + \underbrace{(\theta - \hat{\theta}^i)^\top \nabla_\theta \mathcal{L}^i(\hat{\theta}^i)}_{(b)} + \underbrace{\frac{1}{2}(\theta - \hat{\theta}^i)^\top \mathbf{H}^i (\theta - \hat{\theta}^i)}_{(c)}
\tag{1} L j − 1 prox ( θ ) = i = 1 ∑ j − 1 ( a ) L i ( θ ^ i ) + ( b ) ( θ − θ ^ i ) ⊤ ∇ θ L i ( θ ^ i ) + ( c ) 2 1 ( θ − θ ^ i ) ⊤ H i ( θ − θ ^ i ) ( 1 ) 其中,(a) 是在最优参数处的损失值,(b) 是一阶导数项,(c) 是二阶海森矩阵项,用于捕捉参数变化带来的曲率影响。这里的 a 和 θ \theta θ
命题 1 :在基于正则化的连续学习中,若模型参数 θ \theta θ ∪ i = 1 j − 1 N i \cup_{i=1}^{j-1} \mathcal{N}^i ∪ i = 1 j − 1 N i N i = { θ : d ( θ , θ ^ i ) < δ i } \mathcal{N}^i = \{\theta : d(\theta, \hat{\theta}^i) < \delta^i\} N i = { θ : d ( θ , θ ^ i ) < δ i } θ \theta θ
θ : = θ − α ( H 1 + H 2 + ⋯ + H j − 1 ) − 1 ∇ θ L j ( θ ) . (2) \theta := \theta - \alpha (\mathbf{H}^1 + \mathbf{H}^2 + \cdots + \mathbf{H}^{j-1})^{-1} \nabla_\theta \mathcal{L}^j(\theta). \tag{2} θ := θ − α ( H 1 + H 2 + ⋯ + H j − 1 ) − 1 ∇ θ L j ( θ ) . ( 2 ) 连续学习中海森矩阵的作用# : 令 H = ∑ i = 1 j − 1 H i \mathbf{H} = \sum_{i=1}^{j-1} \mathbf{H}^i H = ∑ i = 1 j − 1 H i H \mathbf{H} H H \mathbf{H} H ∇ θ L j ( θ ) \nabla_\theta \mathcal{L}^j(\theta) ∇ θ L j ( θ ) H \mathbf{H} H
NOTE 假设海森矩阵 H \mathbf{H} H
H = U Λ U ⊤ \mathbf{H} = U \Lambda U^\top H = U Λ U ⊤
其中:
U = [ u 1 , u 2 , … , u n ] U = [\mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_n] U = [ u 1 , u 2 , … , u n ] Λ = diag ( λ 1 , λ 2 , … , λ n ) \Lambda = \text{diag}(\lambda_1, \lambda_2, \ldots, \lambda_n) Λ = diag ( λ 1 , λ 2 , … , λ n ) λ 1 ≥ λ 2 ≥ … ≥ λ n ≥ 0 \lambda_1 \geq \lambda_2 \geq \ldots \geq \lambda_n \geq 0 λ 1 ≥ λ 2 ≥ … ≥ λ n ≥ 0 更新公式中的关键项是:
H − 1 ∇ θ L j ( θ ) = U Λ − 1 U ⊤ ∇ θ L j ( θ ) \mathbf{H}^{-1} \nabla_\theta \mathcal{L}^j(\theta) = U \Lambda^{-1} U^\top \nabla_\theta \mathcal{L}^j(\theta) H − 1 ∇ θ L j ( θ ) = U Λ − 1 U ⊤ ∇ θ L j ( θ )
将梯度投影到特征向量方向上:
∇ θ L j ( θ ) = ∑ i = 1 n ( ∇ θ L j ( θ ) ⊤ u i ) u i = ∑ i = 1 n g i u i \nabla_\theta \mathcal{L}^j(\theta) = \sum_{i=1}^n (\nabla_\theta \mathcal{L}^j(\theta)^\top \mathbf{u}_i) \mathbf{u}_i = \sum_{i=1}^n g_i \mathbf{u}_i ∇ θ L j ( θ ) = ∑ i = 1 n ( ∇ θ L j ( θ ) ⊤ u i ) u i = ∑ i = 1 n g i u i
其中 g i = ∇ θ L j ( θ ) ⊤ u i g_i = \nabla_\theta \mathcal{L}^j(\theta)^\top \mathbf{u}_i g i = ∇ θ L j ( θ ) ⊤ u i i i i
H − 1 ∇ θ L j ( θ ) = ∑ i = 1 n g i λ i u i \mathbf{H}^{-1} \nabla_\theta \mathcal{L}^j(\theta) = \sum_{i=1}^n \frac{g_i}{\lambda_i} \mathbf{u}_i H − 1 ∇ θ L j ( θ ) = ∑ i = 1 n λ i g i u i
” 在大特征值方向上被抑制 ” 指的是:
大特征值方向 :当 λ i \lambda_i λ i g i λ i \frac{g_i}{\lambda_i} λ i g i 小特征值方向 :当 λ i \lambda_i λ i g i λ i \frac{g_i}{\lambda_i} λ i g i 统一框架下的基于正则化的持续学习 : 鉴于海森矩阵在模型更新中的重要作用,各种正则化的方法主要致力于改进海森矩阵的近似,比如 EWC 和 On-EWC 使用对角 fihser 矩阵来近似海森矩阵,此外还有因子分解拉普拉斯近似等方法.
从海森近似角度重新审视元持续学习# 具体而言,虽然基于正则化的方法显式地近似二阶海森矩阵,但 Meta-CL 通过超梯度的计算来利用二阶信息。
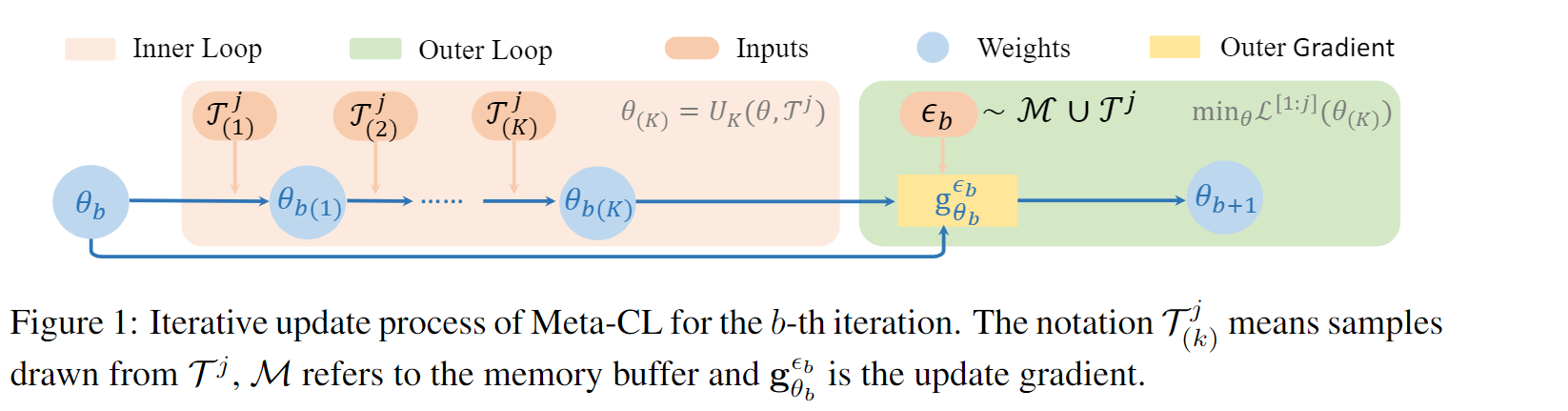
元学习# Riemer 等人提出了元学习框架,旨在最小化所有已见任务 T [ 1 : j ] T^{[1:j]} T [ 1 : j ] M \mathcal{M} M
min θ L [ 1 : j ] ( θ ( K ) ) s.t. θ ( K ) = U K ( θ ; T j ) , w h e r e U K ( θ ; T j ) = U ∘ ⋯ ∘ U ⏟ K inner steps ( U ( θ ( 0 ) ; T ( 0 ) j ) ) , U ( θ ( k ) ; T ( k ) j ) = [ θ − β ∇ θ L ( k ) j ( θ ) ] ∣ θ = θ ( k − 1 ) \begin{align}
\min_{\theta} \mathcal{L}^{[1:j]}(\theta_{(K)}) \quad \text{s.t.} \quad \theta_{(K)} = U_K(\theta; \mathcal{T}^j), \\
where U_K(\theta; \mathcal{T}^j) = \underbrace{U \circ \cdots \circ U}_{K \text{ inner steps}} (U(\theta_{(0)}; \mathcal{T}^j_{(0)})), U(\theta_{(k)}; \mathcal{T}^j_{(k)}) = [\theta - \beta \nabla_\theta \mathcal{L}^j_{(k)}(\theta)]|_{\theta=\theta_{(k-1)}} \tag{3}
\end{align} θ min L [ 1 : j ] ( θ ( K ) ) s.t. θ ( K ) = U K ( θ ; T j ) , w h ere U K ( θ ; T j ) = K inner steps U ∘ ⋯ ∘ U ( U ( θ ( 0 ) ; T ( 0 ) j )) , U ( θ ( k ) ; T ( k ) j ) = [ θ − β ∇ θ L ( k ) j ( θ )] ∣ θ = θ ( k − 1 ) ( 3 ) L [ 1 : j ] ( θ ( K ) ) \mathcal{L}^{[1:j]}(\theta_{(K)}) L [ 1 : j ] ( θ ( K ) ) θ ( K ) \theta_{(K)} θ ( K ) j j j T [ 1 : j ] T^{[1:j]} T [ 1 : j ] T j T^j T j M \mathcal{M} M θ ( k ) \theta_{(k)} θ ( k ) T j T^j T j k k k U ( ⋅ ) U(\cdot) U ( ⋅ )
在外部循环中,我们从 T j T^j T j M \mathcal{M} M ϵ b \epsilon_b ϵ b L [ 1 : j ] ( θ b ( K ) ) \mathcal{L}^{[1:j]}(\theta_{b(K)}) L [ 1 : j ] ( θ b ( K ) ) θ b \theta_b θ b g θ b ϵ b : = ∂ L ( θ b ( K ) ; ϵ b ) / ∂ θ b g^{\epsilon_b}_{\theta_b} := \partial \mathcal{L}(\theta_{b(K)}; \epsilon_b)/\partial \theta_b g θ b ϵ b := ∂ L ( θ b ( K ) ; ϵ b ) / ∂ θ b θ b \theta_b θ b g θ b ϵ b g^{\epsilon_b}_{\theta_b} g θ b ϵ b 说白了就是内循环中,拷贝当前模型的一个备份,进行 n 次训练后再拿到外循环中计算一个大的 loss 来更新原始模型
海森近似角度重新审视元持续学习# 为了解决上面的公式 3 中的双重优化,我们需要计算 L [ 1 : j ] ( θ ( K ) ) \mathcal{L}^{[1:j]}(\theta_{(K)}) L [ 1 : j ] ( θ ( K ) ) θ \theta θ
∂ L [ 1 : j ] ( θ ( K ) ) ∂ θ = ∂ L [ 1 : j ] ( θ ( K ) ) ∂ θ ( K ) ∂ θ ( K ) ∂ θ , \frac{\partial \mathcal{L}^{[1:j]}(\theta_{(K)})}{\partial \theta} = \frac{\partial \mathcal{L}^{[1:j]}(\theta_{(K)})}{\partial \theta_{(K)}} \frac{\partial \theta_{(K)}}{\partial \theta}, ∂ θ ∂ L [ 1 : j ] ( θ ( K ) ) = ∂ θ ( K ) ∂ L [ 1 : j ] ( θ ( K ) ) ∂ θ ∂ θ ( K ) , 其中第一项在 θ \theta θ
∂ L [ 1 : j ] ( θ ( K ) ) ∂ θ ( K ) = ∇ θ ( K ) L [ 1 : j ] ( θ ( K ) ) ≈ ∇ θ ( K ) L [ 1 : j ] ( θ ) + H M j ( θ ( K ) − θ ) + ( θ ( K ) − θ ) T ⊗ T ⊗ ( θ ( K ) − θ ) . \frac{\partial \mathcal{L}^{[1:j]}(\theta_{(K)})}{\partial \theta_{(K)}} = \nabla_{\theta_{(K)}} \mathcal{L}^{[1:j]}(\theta_{(K)}) \approx \nabla_{\theta_{(K)}} \mathcal{L}^{[1:j]}(\theta) + \mathbf{H}_M^j (\theta_{(K)} - \theta) + (\theta_{(K)} - \theta)^T \otimes \mathbf{T} \otimes (\theta_{(K)} - \theta). ∂ θ ( K ) ∂ L [ 1 : j ] ( θ ( K ) ) = ∇ θ ( K ) L [ 1 : j ] ( θ ( K ) ) ≈ ∇ θ ( K ) L [ 1 : j ] ( θ ) + H M j ( θ ( K ) − θ ) + ( θ ( K ) − θ ) T ⊗ T ⊗ ( θ ( K ) − θ ) . 注意,H M j = ∇ θ ( K ) 2 L [ 1 : j ] ( θ ) \mathbf{H}_M^j = \nabla_{\theta_{(K)}}^2 \mathcal{L}^{[1:j]}(\theta) H M j = ∇ θ ( K ) 2 L [ 1 : j ] ( θ ) T \mathbf{T} T ⊗ \otimes ⊗ T j T^j T j K = 1 K=1 K = 1
这里我们希望找到一个最优解 θ ∗ \theta^* θ ∗ ∂ L [ 1 : j ] ( θ ( K ) ) ∂ θ = 0 \frac{\partial \mathcal{L}^{[1:j]}(\theta_{(K)})}{\partial \theta}=0 ∂ θ ∂ L [ 1 : j ] ( θ ( K ) ) = 0 ∂ L [ 1 : j ] ( θ ( K ) ) ∂ θ ( K ) = 0 \frac{\partial \mathcal{L}^{[1:j]}(\theta_{(K)})}{\partial \theta_{(K)}}=0 ∂ θ ( K ) ∂ L [ 1 : j ] ( θ ( K ) ) = 0
命题 2 :对于具有单次内循环适应的 Meta-CL,假设 θ ( K ) \theta_{(K)} θ ( K ) θ ∗ = arg min θ L [ 1 : j ] ( θ ( K ) ) \theta^* = \arg\min_\theta \mathcal{L}^{[1:j]}(\theta_{(K)}) θ ∗ = arg min θ L [ 1 : j ] ( θ ( K ) ) ϵ \epsilon ϵ N ( θ ∗ , ϵ ) N(\theta^*, \epsilon) N ( θ ∗ , ϵ ) L \mathcal{L} L μ \mu μ β < δ / ∣ ∇ θ L j ( θ ) − ( ∇ θ L j ( θ ) ) 2 ∣ \beta < \sqrt{\delta / |\nabla_\theta \mathcal{L}^j(\theta) - (\nabla_\theta \mathcal{L}^j(\theta))^2|} β < δ /∣ ∇ θ L j ( θ ) − ( ∇ θ L j ( θ ) ) 2 ∣ δ \delta δ α = β 2 \alpha = \beta^2 α = β 2
θ : = θ − α ( H M j ) − 1 ∇ θ L j ( θ ) . \theta := \theta - \alpha (\mathbf{H}_M^j)^{-1} \nabla_\theta \mathcal{L}^j(\theta). θ := θ − α ( H M j ) − 1 ∇ θ L j ( θ ) . 上述表示这个超梯度方法实际上隐式等价与使用海森矩阵并遵循基于正则化的方法的归一迭代.比对俩个命题,我们能发现:Meta-CL 利用从记忆缓冲区 M \mathcal{M} M H M j \mathbf{H}_M^j H M j ( H 1 + H 2 + ⋯ + H j − 1 ) (\mathbf{H}^1 + \mathbf{H}^2 + \cdots + \mathbf{H}^{j-1}) ( H 1 + H 2 + ⋯ + H j − 1 ) H i \mathbf{H}^i H i H M j \mathbf{H}_M^j H M j
尽管 Meta-CL 通过记忆缓冲区 M \mathcal{M} M M \mathcal{M} M
元学习中的方差缩减# 对于元学习中随机抽取策略带来的高方差,本文提出了方差缩减元持续学习,这种超梯度策略的方差缩减等价于在海森矩阵上添加正则化项.
方差缩减元持续学习# VR-MCL 旨在通过减少超梯度的方差来降低其隐式估计的海森矩阵的方差。在在线持续学习设置中,任务中的样本是以小批量形式接收的,且无法访问完整的样本集,这给这些技术的实施带来了挑战.
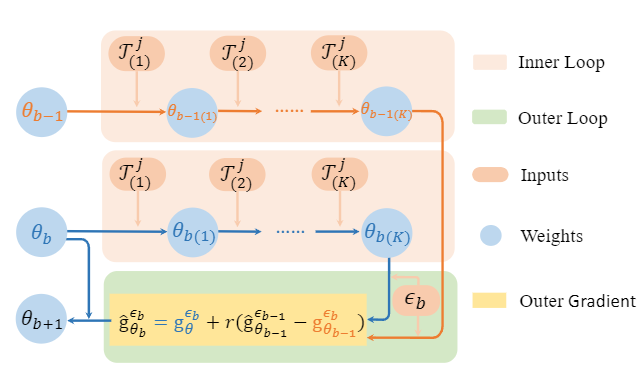
基于此,我们提出了基于动量的方差减小元持续学习方法,该方法不用计算全部的梯度,而是保留先前步骤中的模型.其中 g ^ θ b − 1 ϵ b − 1 \hat{\mathbf{g}}_{\theta_{b-1}}^{\epsilon_b-1} g ^ θ b − 1 ϵ b − 1 g θ b − 1 ϵ b \mathbf{g}_{\theta_{b-1}}^{\epsilon_b} g θ b − 1 ϵ b g θ b ϵ b \mathbf{g}_{\theta_b}^{\epsilon_b} g θ b ϵ b ϵ b \epsilon_b ϵ b θ b − 1 \theta_{b-1} θ b − 1 θ b \theta_b θ b r r r
g ^ θ b ϵ b = g θ b ϵ b + r ( g ^ θ b − 1 ϵ b − 1 − g θ b − 1 ϵ b ) . ( 4 ) \hat{\mathbf{g}}_{\theta_b}^{\epsilon_b} = \mathbf{g}_{\theta_b}^{\epsilon_b} + r\left(\hat{\mathbf{g}}_{\theta_{b-1}}^{\epsilon_{b-1}} - \mathbf{g}_{\theta_{b-1}}^{\epsilon_b}\right).
\quad (4) g ^ θ b ϵ b = g θ b ϵ b + r ( g ^ θ b − 1 ϵ b − 1 − g θ b − 1 ϵ b ) . ( 4 ) 为了理解为什么公式 (4) 能够产生更小的梯度方差,我们首先考察误差项 Δ b : = g ^ θ b ϵ b − G θ b \Delta_b := \hat{\mathbf{g}}_{\theta_b}^{\epsilon_b} - G_{\theta_b} Δ b := g ^ θ b ϵ b − G θ b g ^ θ b ϵ b \hat{\mathbf{g}}_{\theta_b}^{\epsilon_b} g ^ θ b ϵ b G θ b G_{\theta_b} G θ b E [ ∥ Δ b ∥ 2 ] \mathbb{E}[\|\Delta_b\|^2] E [ ∥ Δ b ∥ 2 ] Δ b \Delta_b Δ b
Δ b = r Δ b − 1 + ( 1 − r ) ( g θ b ϵ b − G θ b ) + r ( g θ b ϵ b − g θ b − 1 ϵ b − ( G θ b − G θ b − 1 ) ) . ( 5 ) \Delta_b = r\Delta_{b-1} + (1-r)(\mathbf{g}_{\theta_b}^{\epsilon_b} - G_{\theta_b}) + r(\mathbf{g}_{\theta_b}^{\epsilon_b} - \mathbf{g}_{\theta_{b-1}}^{\epsilon_b} - (G_{\theta_b} - G_{\theta_{b-1}})).
\quad (5) Δ b = r Δ b − 1 + ( 1 − r ) ( g θ b ϵ b − G θ b ) + r ( g θ b ϵ b − g θ b − 1 ϵ b − ( G θ b − G θ b − 1 )) . ( 5 ) 第二项 ( 1 − r ) ( g θ b ϵ b − G θ b ) (1-r)(\mathbf{g}_{\theta_b}^{\epsilon_b} - G_{\theta_b}) ( 1 − r ) ( g θ b ϵ b − G θ b ) r r r g θ b ϵ b − g θ b − 1 ϵ b − ( G θ b − G θ b − 1 ) \mathbf{g}_{\theta_b}^{\epsilon_b} - \mathbf{g}_{\theta_{b-1}}^{\epsilon_b} - (G_{\theta_b} - G_{\theta_{b-1}}) g θ b ϵ b − g θ b − 1 ϵ b − ( G θ b − G θ b − 1 ) μ \mu μ L \mathcal{L} L O ( ∥ θ b − θ b − 1 ∥ ) = O ( α ∥ g ^ θ b − 1 ϵ b − 1 ∥ ) O(\|\theta_b - \theta_{b-1}\|) = O(\alpha\|\hat{\mathbf{g}}_{\theta_{b-1}}^{\epsilon_{b-1}}\|) O ( ∥ θ b − θ b − 1 ∥ ) = O ( α ∥ g ^ θ b − 1 ϵ b − 1 ∥ ) ∥ Δ b ∥ = r ∥ Δ b − 1 ∥ + S \|\Delta_b\| = r\|\Delta_{b-1}\| + S ∥ Δ b ∥ = r ∥ Δ b − 1 ∥ + S S S S r r r α \alpha α ∥ Δ b ∥ \|\Delta_b\| ∥ Δ b ∥ S / ( 1 − r ) S/(1-r) S / ( 1 − r ) r r r α \alpha α S / ( 1 − r ) S/(1-r) S / ( 1 − r )
VR-MCL 的理论证明# 定理 1(VR-MCL 的遗憾界) 。在线持续学习中的遗憾定义为 C R j = F ~ ( θ ) − F ( θ ∗ ) \mathbf{CR}_j = \tilde{F}(\theta) - F(\theta^*) CR j = F ~ ( θ ) − F ( θ ∗ ) F ~ ( θ ) = ∑ i = 1 j L i ( θ ^ i ) \tilde{F}(\theta) = \sum_{i=1}^{j} \mathcal{L}^i(\hat{\theta}^i) F ~ ( θ ) = ∑ i = 1 j L i ( θ ^ i ) F ( θ ∗ ) = min θ ∑ i = 1 j L i ( θ ) F(\theta^*) = \min_\theta \sum_{i=1}^{j} \mathcal{L}^i(\theta) F ( θ ∗ ) = min θ ∑ i = 1 j L i ( θ ) F F F φ \varphi φ μ \mu μ G G G η \eta η σ \sigma σ M M M T T T δ ∈ ( 0 , 1 ) \delta \in (0,1) δ ∈ ( 0 , 1 ) 1 − δ 1-\delta 1 − δ
C R j ≤ ( log T + 1 ) ( F ( θ 1 ) − F ( θ ∗ ) ) + L D 2 ( log T + 1 ) 2 2 + L D 2 ( log T + 1 ) 2 2 + ( 16 L D 2 + 16 σ D + 4 M ) 2 T log ( 8 T / δ ) = O ~ ( T ) . \mathbf{CR}_j \leq (\log T + 1)(F(\theta_1) - F(\theta^*)) + \frac{LD^2(\log T + 1)^2}{2}
+ \frac{LD^2(\log T + 1)^2}{2} + (16LD^2 + 16\sigma D + 4M)\sqrt{2T\log(8T/\delta)} = \tilde{O}(\sqrt{T}). CR j ≤ ( log T + 1 ) ( F ( θ 1 ) − F ( θ ∗ )) + 2 L D 2 ( log T + 1 ) 2 + 2 L D 2 ( log T + 1 ) 2 + ( 16 L D 2 + 16 σ D + 4 M ) 2 T log ( 8 T / δ ) = O ~ ( T ) . 定理 1 说明 ,在随机设置下,只要满足一些温和的假设条件,VR-MCL 算法能够以高概率(w.h.p.)达到近似最优的 O ~ ( T ) \tilde{O}(\sqrt{T}) O ~ ( T )
-7561599.D_DtiG-O_ONURN.webp)
