Embracing Unimodal Aleatoric Uncertainty for Robust Multimodal Fusion

2024-10-10

/

/

Abstract#

作为一个多模态学习的基础任务,多模态融合旨在补充单模态的限制.其中一个特征融合的挑战是:大多数的单模态数据在他们的特征空间中都包含了潜在的噪声,可能会影响多模态的交互.在这篇文章中,我们说明了单模态的潜在噪声可以被量化甚至通过对比学习来进一步的增强单模态嵌入的稳定性.特定的来说,我们提出了一种新的通用鲁棒多模态融合策略,叫做Embracing Aleatoric Uncertainty(EAU).它包含了两个主要步骤:1. 稳定的单模态特征增强（SUFA） 2)鲁棒的多模态特征聚合(SUFA)

Introduction#

通过利用来自不同模态的互补信息,多模态学习在 AI 应用上取得了 success,多模态特征融合成为了一个主要的研究方向.

然而,研究者发现来自不同模态的信息也许是不可靠的,因为他们在自己的空间中都包含了一定的噪声.最近的部分研究表明先前的特征融合方式也许会因为多模态的交互被数据中的不确定性影响而失败.如下图所示,因为正类的含义是 fuzzy 的并且 label 也是被 human 主观判断的,所以其中存在不小的噪声.一般来说，我们可以说引入的噪声来自于异质的不确定性，它削弱了利用多模态数据的有效性，并证明了多模态学习不是一个免费的午餐

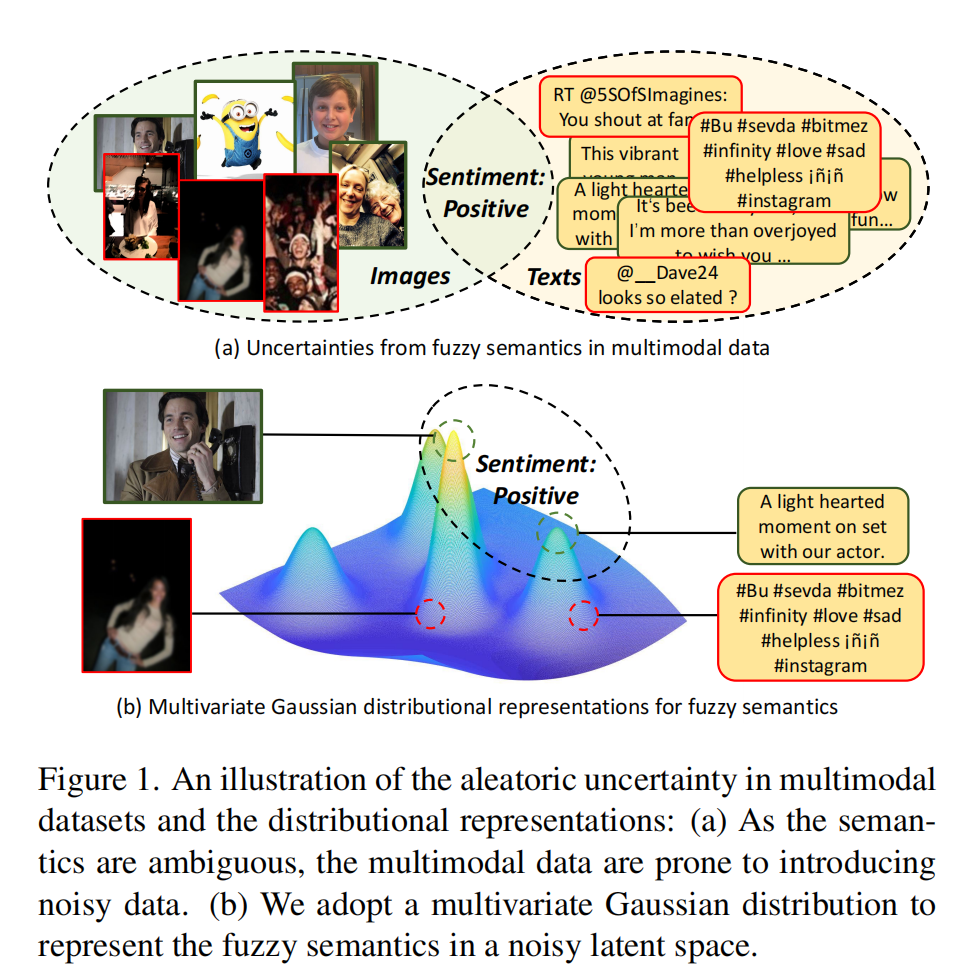
因此,随着多模态不确定性的挑战,我们提出了第一个基础问题:我们能否量化多模态数据中的不确定性? 我们假设每个 instance 都能被一个多元标准正态分布所表示,其中方差可以看做是内在的不确定性.有了量化的不确定性,我们可以提出第二个问题:完全抛弃内在的不确定性是否合适? 从图一中我们可以看到即使是 image-text pair,由于域偏移,额外描述甚至是图片质量问题,异质不确定性是不可避免的.为此，如图 1(b)所示，我们认为考虑异质不确定性的多元正态分布可以被视为语义的模糊表示，其中与语义相关的数据在相似的分布中，即使它们处于不同的模式。在这两个假设的激励下，本文开发了一种新的多模态融合策略，即拥抱弹性不确定性（EAU）。

特定来说,我们的 EAU 模型包含了以下两个步骤

稳定的单模态特征增强(SUFA)通过把每个实例转换为多元高斯正态分布量化了每个模态的内在异质不确定性,然后我们使用自监督对比学习来增强单模态嵌入.
鲁棒的多模态特征融合(RMFI)动态的把稳定的单模态嵌入到一个联合的表示.特定来说,考虑到 SUFA 只考虑了语义一致性而忽略了信息冗余的问题,我们采用了一种信息理论的策略,Variational Information Bottleneck 来学习一个紧凑的联合表示来减少信息冗余.

多模态融合,多模态融合旨在从不同模态中学习一个更强的表示.通常来说,信息融合有 3 类,早起融合,中间融合和晚期融合.先前的多模态融合方法被归类为早/晚融合根据他们的特征 level 和决策 level 的融合操作.在过去的 decades 中,大量的任务认为中间融合(学习一个多模态数据的统一嵌入)能够帮助表征学习.虽然大量的工作都取得了很好的效果,但是他们都忽略了多模态学习的不确定性问题.最近的一些任务证明了传统的特征融合方法对于噪声的鲁棒性和适应性只有有限的效果.基于此,我们发明了一种能够量化不确定性和学习更为鲁棒表示的方法.

深度学习的不确定性:总的来说,深度学习中的不确定性可以被分为认知不确定性和异质不确定性.前者旨在捕捉神经网络参数中的噪声,而后者测量给定数据中的噪声.为了提升开放世界中的鲁棒性和泛化性,许多研究人员把不确定评估也纳入了深度学习中,但是他们大多只量化了不确定性来学习夸模态交互的概率分布表示,而忽略了内存不确定性的价值和模态融合的鲁棒性.

Information Bottleneck Theory:信息瓶颈理论最初在信号处理中被提出的,给定一个信号的最简洁表示并且保留最大的信息.vib 被提出来成为这个理论和深度学习之间的桥梁.

Proposed Mehtod#

准备工作#

深度学习模型中的不确定性估计:两种不确定性异质和认知,前者是观察中存在的不确定性无法被更多数据解释,而后者是在模型中的不确定性,可以用更多数据来解释.总的来说,给定一个模型 $f_{\theta}(\cdot)$ 并且将 x->y,x 中的随机不确定性会导致 y 的预测失败.为了削减这种不确定性,一种广泛采取的策略是使用 dropout 操作来对不同的预测采用 n 次权重 $\theta \sim p(\theta|x,y)$ 来获得均值和方差.在这里我们可以预测方差来得到 x 的不确定性

\begin{align} \mu_{*}^2(x) = \frac{1}{N} \sum_i \mu_i^2(x)\\ \sigma_{*}^2(x) = \frac{1}{N} \sum_i \sigma_i^2(x) + \frac{1}{N} \sum_i \mu_i^2(x) - \mu_{*}^2(x)\\ = \mathbb{E}_i[\sigma_i^2(x)] + \text{Var}_i[\mu_i(x)]. \end{align}

其中 $\mathbb{E}_i[\sigma_i^2(x)]$ 是异质不确定性, $\text{Var}_i[\mu_i(x)]$ 是认知不确定性,这是模型的而不是数据的.在本文中我们更多考虑异质不确定性

在这里一个是样本方差的期望,表示样本的内在不确定性,一个是样本均值的方差,这是模型的不确定性

变分信息瓶颈#

变分信息瓶颈是深度学习中常用的策略,保持特征的最大信息并且冗余小.具体来说,给定一个有冗余信息的输入变量 x 和一个 target y.VIB 希望学习一个紧凑的潜在变量 Z, 并且 z 能够最大限度的描述目标 y.此外,由于 x 是冗余的,z 需要能够对 x 最小鉴别.在我们的工作中,我们利用 vib 来学习一个紧凑的联合表示,克服了高度对齐的多模态表示带来的融合来提升多模态融合的鲁棒性.

稳定的单模态表示#

由于不同的模态数据在他们的空间中包含独自的噪声,我们首先提出了稳定的单模态增强模块来量化他们的不确定性.

单模态分布表示:给定一个多模态样本 $x_i^m$ ,m 的模态可以是图片,文本,音频等.我们学习分布表示来量化每个模态中的任意不确定性。根据上面的公式,如果不考虑认知不确定性,我们可以使用模型的方差来预测异质不确定性.基于此,我们首先使用对应的特征提起去来学习每个模态的初识 embedding,然后使用 2 个全连接层学习均值和方差.

此外,我们定义每个样本的特征空间中的表示 z 为 d 个参数的多元高斯分布,可以表示为

p(z_i^m | x_i^m) \sim \mathcal{N}(\mu_i^m, \sigma_i^{m2} \mathbf{I})\\ \quad \mu_i^m = f_{\theta_1^m}(x_i^m), \quad \sigma_i^m = f_{\theta_2^m}(x_i^m),

其中两个 f 是不同的全连接层.为了保持每个模态的语义一致性,我们进一步将多模态样本的分布表示用 KL 散度对齐：

L_{\text{UDR}} = \sum_{\substack{m_1, m_2 \in \mathcal{M} \\ m_1 \neq m_2}} KL \left( p(z_i^{m_1} | x_i^{m_1}) \| p(z_i^{m_2} | x_i^{m_2}) \right)\\ + \sum_{m \in \mathcal{M}} KL \left( p(z_i^{m} | x_i^{m}) \| \mathcal{N}(0, \mathbf{I}) \right).

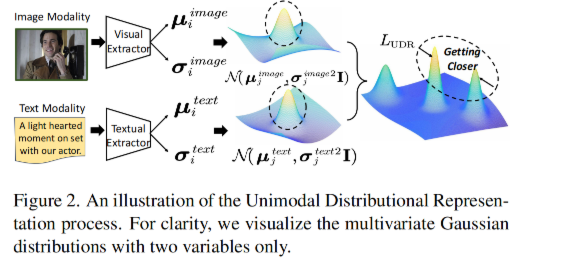由图二我们可以看出 $L_{udr}$ 可以让相同语义的两个模态的分布更加靠近.这样,每个多模态样本的表示就不局限于一个点的 embedding,而是对几个多元高斯分布的模糊表示.特别的是,方差揭露了 m 个模态中的异质不确定性而均值是对应的稳定表示.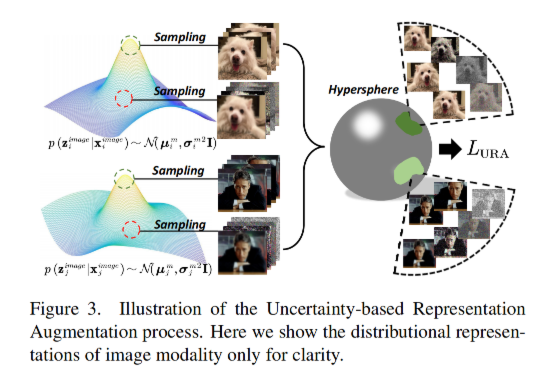

总之,上面的意思就是我们把样本转换为了高斯分布,然后使用那个算法把多元的表示变成了一个多元高斯分布,这样就变成了一个范围而不是单一的 embedding.并且其中的方差是不确定性,均值是稳定的表示.

基于不确定性的表现增强:我们有了异质不确定性的量化,第二个问题就诞生了:我们应该扔掉多元数据中的不确定性吗?直觉上来说,异质不确定性是无法避免的因为语义的天然的歧义.但是这也导致了不同模态中的单模态数据的多样性.基于此,我们利用噪声生成了看不见的样本这样，学习到的单模态表示对具有相似语义的不同单模态输入不敏感。对于前面得到的 zi,我们积极从中采样一个 anchor point(头上戴波浪号)和一个 augmented point,此外，我们从其他分布表示中随机抽取一组负点，并设计了一种自监督的对比学习机制如下：

L_{\text{URA}} = -\log \frac{e^{\text{sim}(\tilde{z}_i^m, z_i^m)/\tau}}{\sum_{j \neq i} \left( e^{\text{sim}(\tilde{z}_i^m, z_i^m)/\tau} + e^{\text{sim}(\tilde{z}_i^m, z_j^m)/\tau} \right)}

鲁棒的多模态特征表示#

随着 SUFA,我们获得了具有语义一致性的稳定的单峰表示,但是我们只考虑的语义一致性而忽略了特征冗余.因此我们提出了 RMFI 模块 动态特征集成:被动态多模态融合启发,我们假设不同的模态对于最终的联合表现的贡献是不一样的,因此我们基于 attention 开发了动态多模态结合策略,具体来说,给定一个稳定的单模态表示 $\mu$ ,我们基于他们的量化不确定性来给定不同的权重

\hat{x}_i = \sum_{m \in M} \alpha_i^m \mu_i^m, \alpha_i^m = \frac{e^{\frac{1}{\sigma_i^m}}}{\sum_{m \in M} e^{\frac{1}{\sigma_i^m}}}

通过这种方式,我们计算出了一个联合的表示,其中每个模态的贡献是动态计算的. 联合表示的压缩:我们设计了一个具有 VIB 的联合表示压缩器.这里我们提出了两种不同的针对下游任务的损失函数.

总结#

总的来说,这篇文章首先提出了对于模型中存在的噪声的问题,也就是认知不确定和异质不确定.我们首先通过特城提取器+两个fc层得到样本的均值和方差,然后用一个高斯分布表示每一个样本.然后使用一个函数将多模态输入的分布进行对齐,让每个样本不是一个embedding,而是几个分布的联合表示.而后,我们使用对比学习的方式来增强特征的表示,从而利用了异质不确定性而不是丢弃这些噪声.而后,我们使用动态特征集成得到一个线性和,最终再进行特征压缩.